まいど!
前回の記事で、グラフの平行移動の問題を解説したわけやけど、
(言うても、特に解説らしきことはしてへんなw)
そのグラフの平行移動の話で、ジブンが
「x軸方向に+aするとxを(x-a)に、y軸方向に+bするとyを(y-b)に置き換える」
っていうやつ、
丸暗記してるし、やれっていわれたら出来るけど、なんでそうなるんかわからん
という状況やったりするかもしれへんなあと思ったから、解説するわ。2通りの解説。
誰もが説明する模範解答と、逆転の発想の解説な。
2番目の方がわかりやすいって思ってもらえたら、むっちゃ嬉しいわ。
もう、それこそ、死んでもええくらいに嬉しいわ。
あ、ワシ1901年2月3日に死んでるんやった。(てへぺろ
ちなみに、合格するのに必須の話 ではないで。
上の赤字蛍光ペンの部分覚えればエエし、
なんでそうなるん?とか思ってなかったら読む必要ないで。
模範的解説
一般的な受験数学でいうところの数2の「軌跡と領域」の考え方や。
一般曹候補生の範囲外ではあるけど、そんなムズないで。
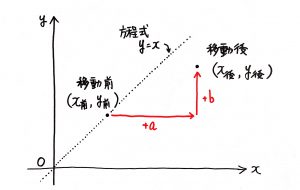
移動前の点\((x_{前},y_{前})\)があるとして、
x軸方向に+a, y軸方向に+bしたとしよう。
変に難しくならんように、グラフの方程式はy=xにしとくで。
こういうことな。
3STEPsで考えるで。
<1> 平行移動前の点と、平行移動後の点の関係を式にする
<2>平行移動前の点 = の形にする
<3>平行移動前の方程式に、<2>を代入する
ほな、みていこか。
迷ったら上の図に戻ってみてや。
<1>平行移動前の点と、平行移動後の点の関係を式にする
\(x_{前}\)に+aして、\(y_{前}\)に+bしたら、移動後の新しい点が出てくるわけやから
\( x_{後} = x_{前} + a\)
\( y_{後} = y_{前} + b\)
やな。
<2>平行移動前の点 = の形にする
カンタン、カンタン。
\( x_{後} = x_{前} + a\)
⇔\( x_{前} = x_{後} – a\)
\( y_{後} = y_{前} + b\)
⇔\( y_{前} = y_{後} – b\)
<3>平行移動前の方程式に、<2>を代入する
カンタン、カンタン、カンタン。
平行移動前の方程式y=xに、<2>を代入するだけな。
\(y_{前} = x_{前}\)
⇔\(y_{後} – b\) = \( x_{後} – a\)
はいできたー!
x軸方向に+aしたらxはx-aになってるし
y軸方向に+bしたらyはy-bになってるな。
ん…?
「何か納得いかん」
「数学的には確かにそうやけど、感覚的にはスッと入ってこないッス」
「福沢諭吉先生がそんなありきたりな解説をする、とるに足らない、つまらない、凡百の先生だとは思っていませんでした。失望しました」
ジブン、言いたい放題やな…。
しゃーないなあ!
逆転の発想の解説
デデーン!
コペルニクスくん的転回や。
結論から言ってしまうと、
グラフを平行移動するんやなくて、グラフ以外を反対向きに平行移動するんや。
グラフ以外って言うても、まあ軸しかないんやけどな。
ちょっとイメージしてみて。
学校の黒板に日本地図貼るやん。まあ、ホワイトボードでもええけど。
ほんでその上に、磁石置くやん。
その磁石を動かすんやなくて、
磁石はそのままで、地図を動かす感じ。
大阪にある磁石を東京に持ってくには、
磁石を右上にググーッと動かしてもええけど、
逆に、地図を左下にズルーッと引っ張ってもええわけやんな。
…おっと?
気づいてしまったジブン「つまりそれって、
グラフをググーッとx軸方向に+aしてもええけど、
逆に、x軸をズルーッと-aしてもええということ…?
じゃあグラフの平行移動って実は
軸の平行移動だと考えられるということ…?!
例えばx軸は、Apple風に言うと「全く新しいx軸」になるということ!
つまり今までのxを、全く新しいxにバージョンアップすればよいのね!
ああ、なるほど!だから、
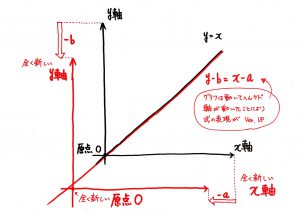
y=xをx軸方向に+a,y軸方向に+bするというのは
x軸を-a,y軸を-bだけズルーッと移動するから
x→x-a,y→y-bにバージョンアップし、
y-b=x-aという全く新しい方程式が得られる。
そう考えればよいのね!
ねえ諭吉先生、そういうことだったのね!?」
諭吉「オーマイガットトゥギャザー!」
-終-