まいど!諭吉です。
幹候生の過去問についてご質問をいただいたんで、シェアするで。
特別に、解説ページもシェアするで。
まずは過去問
解けるかな?
引用元リンクはこちら
https://www.mod.go.jp/gsdf/jieikanbosyu/examination/kakomon/r2_2sikenkyouyou.pdf
諭吉の解説
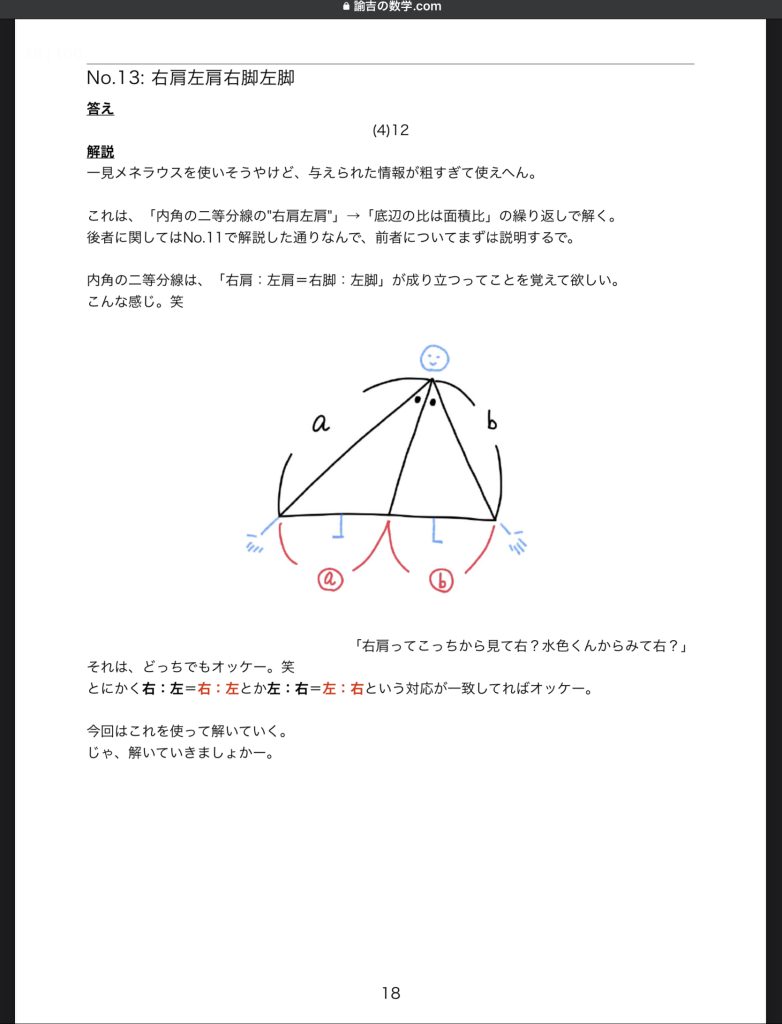
↓
↓
重要なテクニックも少し公開しちゃってますが、
こんなもん極々一部、氷山の一角なんでよいでしょう。笑
いただいたご質問

諭吉の返事
**さん
こんにちは、諭吉です。
テキストをお手に取ってくださってありがとうございます。
ご質問、拝見しました。
結論としては、「数値と比は違う」とご理解いただくと良さそうです。
1. 前提の解説
2. ご質問の解説
3. その次に生まれる質問への解説
という順でお返事しますね。
– – – – – – – – – – – – – – –
1. 前提の解説
数値と比は違うについて
– – – – – – – – – – – – – – –
親から
「3個のアメを、兄と弟で2:1に分けて。」
といわれたら、
兄に2個、弟に1個となりますね。
親が持っているアメの合計が
倍の6個になりました。
親から
「6個のアメを、兄と弟で2:1に分けて。」
といわれたら、
二人がもらうアメの数も倍になるので
兄に4個、弟に2個(、合計6個)となりますね。
この時、
アメの個数(数値)は4:2ですが、
比としてはさっきと同じ2:1ですね。
親が持っているアメがさらに倍になり、
12個になりました。
親から
「12個のアメを、兄と弟で2:1に分けて。」
といわれたら、
二人がもらうアメの数はさらに倍になるので
兄に8個、弟に4個(、合計12個)となりますね。
この時、
アメの個数(数値)は8:4ですが、
比としてはさっきと同じ2:1ですね。
このように、
数値と比はビミョーに異なります。
なので、
比が等しいことと数値が等しいことは、少し違うんです。
上記アメの例では、
8:4=4:2=2:1
という式が成り立ちます。
「8個と4個」も「4個と2個も」
分ける割合(=比)は2:1だからです。
– – – – – – – – – –
2. ご質問の解説
– – – – – – – – – –
ここまでがご理解いただけると、
AB:AC=BQ:QCとなっているためAB=12ならBQ=12にならないか
という部分、
前半では比が等しいという話をしていますが、
後半で数値が等しいという考えに変わってしまっていることが
お分かりいただけるかと思います。
これがもし「AB=BQ」と
「数値が等しい」と言われていたら、
おっしゃる通りAB=12ならBQ=12となります。
ただ今回は「AB:AC=BQ:QC」と
「比が等しい」と言われているだけなので、
AB=12, AC=5なら…
BQ=12, QC=5かもしれないし、
BQ=24, QC=10かもしれないし、
BQ=36, QC=15かもしれないし、
はたまた
BQ=1.2, QC=0.5かもしれません。
ひとまず、
ご質問への直接のお返事はここまでです。
– – – – – – – – – – – – – – – – – – – – –
3. その次に生まれる質問への解説
– – – – – – – – – – – – – – – – – – – – –
オッケー、比はわかった。
じゃあ比がわかってから数値を出すまでは、なんでその式やねん?
というご質問も生まれるかもしれませんので、
解説しておきます。
結論としては、
欲しい数値は、
数値が欲しい方の比
全体の数値×──────────
比の合計
で算出します。
「全体の数値かける『比の合計、ぶんの、数値が欲しい方の比』」です。
1. で解説したアメの例に戻ります。
「12個のアメを、兄と弟で2:1に分けて。」
といわれたら、兄に8個、弟に4個(、合計12個)
となるんでした。
これは、
たとえば兄のアメの個数を出したいときは、
「全体の数値かける『比の合計、ぶんの、数値が欲しい方の比』」
なので、
12×{2/(2+1)}
=12×(2/3)
=8
となります。
ご質問の解説ページの(A)式や、
BQは13×12/17
という計算はそれをしています。
テキスト詳細はこちら
幹候生試験であなたの得点を最大化する戦略
幹部候補生試験の あなたの点数を 今、最大化してみせます 始




