二次関数って解法がたくさんあって困る!二次関数はなんかいろんな形があってどうしたらエエか迷う!
って思ったことない?
おめでとう!
今日はそんなジブンに、プレゼントがあんねん!
二次関数の方位磁石や!
方位磁石はな、
それ自体は答えではないけど、
ジブンが迷った時、
答えにたどり着くために、必要でありがたい代物や。
そんな、二次関数の方位磁石をプレゼントするで!
ほないくで!
二次関数には3パターンの表記がある。
全部、流石に見たことくらいはあるやろ!
- \(y = ax^2 + bx + c\)型
- \(y=a(x-p)^2 + q\)型
- \(y=a(x-p)(x-q)\)型
「こんなん意識してみたことないわ」言う人も、
最後まで読んだらバッチリ意識どころか使い分けれるようになるわ。
シンプルな\(y=ax^2 + bx +c\)型は「方程式」型
二次方程式の問題、つまり式こねくり回すだけの問題、とかは絶対このシンプルな型がエエ。
二次関数の問題、つまりグラフに関連する問題ではあんまりありがたくないわ。
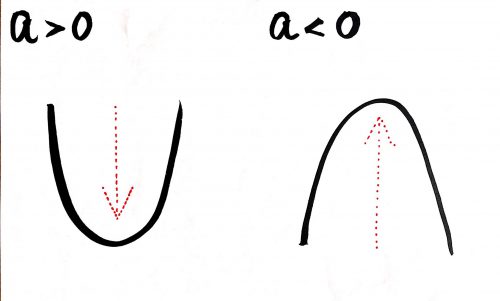
aの値を見て、
a > 0 やったら下に凸, a < 0 やったら上に凸
くらいしか情報が見えへんもん。
でも、「グラフなんてどうでもええから、係数を求めたいんや!」
「連立方程式解きたいんや!」という場合には有効やから、
方程式型 と呼ぶで。
厄介なことにほとんどの問題のスタート地点はこの型やねんな。
でも、グラフ関係の問題は次の2つの型使うんや。
つまり、この型から次の2つの型へは楽勝で変形できなアカンで。
平方完成された\(y=a(x-p)^2 + q\)型は「頂点わかる」型
2次関数の超・重要情報は、頂点と解や。
そのうちの、頂点わかる型がこれや。
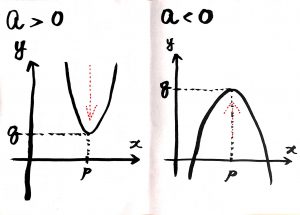
この式から”見える”のは
- どっちに凸か
- 頂点
の二つや。
だからこの形にすれば、
こんなグラフがシュパッ!と描けるわけや!
つまり、頂点(≒最大・最小)に関する問題はこの型に引きずり込めばええねん。
これが迷った時、ジブンを助けてくれる発想やで。
アルファベットがパット見解り辛いから日本語とのハイブリット表記にして最掲するで。
\( y = 凸係数(x-頂点_{のx座標})+頂点_{のy座標}\)
な。
はいオッケー!次ICOCA!
因数分解された\(y=a(x-p)(x-q)\)型は「解見える」型
2次関数の超・重要情報は、頂点と解や。
そのうちの、解わかる型がこれや。
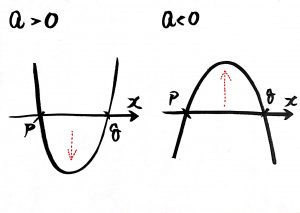
この式から”見える”のは
- どっちに凸か
- 解
の二つや。
だからこの形にすれば、
こんなグラフがシュパッ!と描けるわけや!
つまり、解に関する問題はこの型に引きずり込めばええねん。
これが迷った時、ジブンを助けてくれる発想やで。
アルファベットがパット見解り辛いから日本語とのハイブリット表記すると、
\( y = 凸係数(x-解_{1})(x-解_{2})\)
な。
はいオッケー!
以上3パターン使い分けや。
まとめんで!
\(y=凸x^2+bx+c\)型
- ほとんどの問題でスタート地点
- わかるのは凸の方向
- 方程式問題向き
\(y=凸(x-頂点_{x})^2 + 頂点_{y}\)型
- 平方完成でこの型に持ち込む
- わかるのは凸の方向と、頂点
- グラフの問題で、頂点や最大・最小に関する問題向き
\(y=凸(x-解_{1})(x-解_{2})\)型
- 因数分解でこの型に持ち込む
- わかるのは凸の方向と、解
- グラフの問題で、解系の問題向き
ほな!