まいど!諭吉です。
幹候生の過去問を解いてたらメネラウスの定理を使ったから、
ここでまとめときます。
一応、
- 曹候生
- 航空学生
- 防衛大
- (高等工科は、もしかすると使える問題あるかもレベル)
の範囲でもあるから、それらの受験生もチェックしておいてや。
この定理自体は、小6でも使えるから安心して。
実は、数Bのベクトルの問題も、これで一発ってこともよくあるで。
メネラウスの定理はどんな時に使う?いつ気付く?
メネラウスの定理って何?ってのは後で説明します。
まずは、キツネの顔が見えたら使うってことを覚えて。
どういうことかというと、
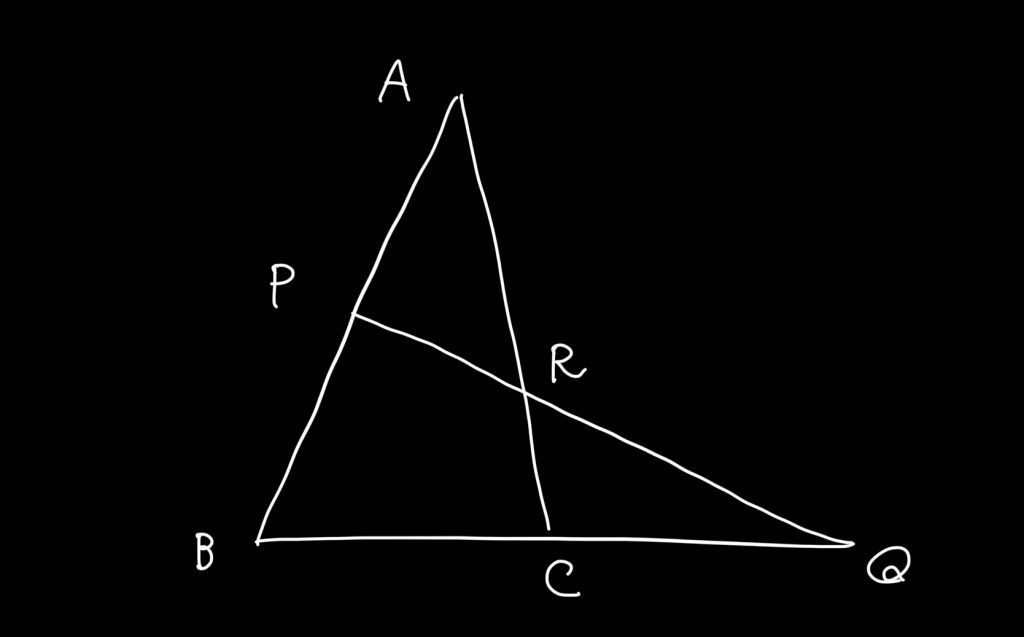
こんな形が出てきたら…
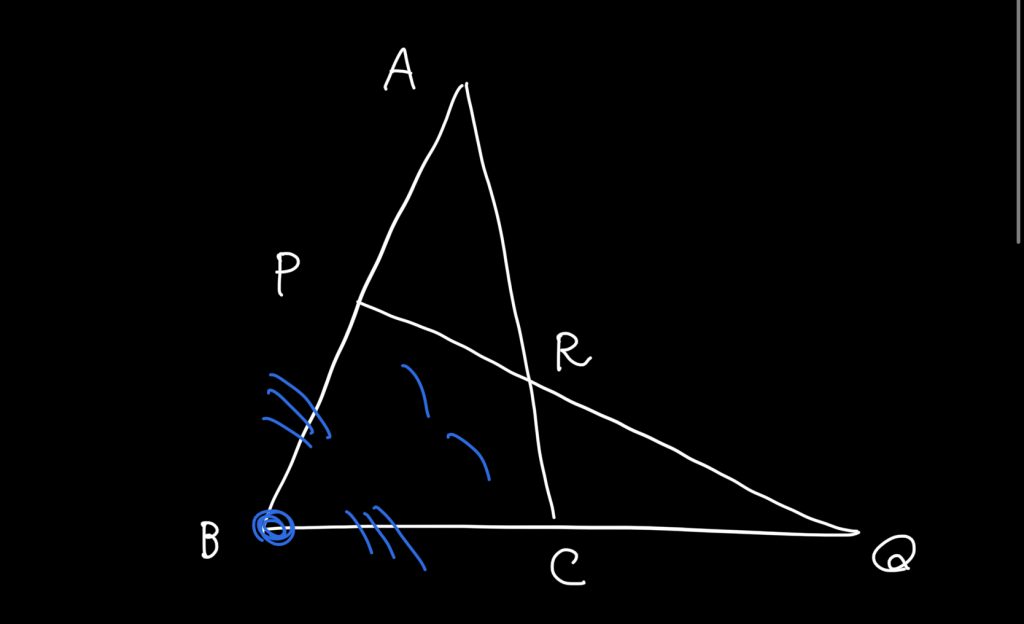
こう見えて欲しいねん🦊w
こんな風に、キツネの顔が見えたら使うのが、メネラウスの定理。
数Bのベクトルの「 t : (1-t) と s : (1-s) とおくやつ」もめんどいことせんでも、これで終わること多いで。
メネラウスの定理の覚え方
定理の式自体はややこしい分数の式やねんけど、あれは覚えなくてエエ。
その代わり、
魔法の5・7・5
「いっこずつ、行って戻って、いっこずつ」
を覚えてw
この5・7・5を唱えながら
キツネちゃんのどちらかの耳→鼻
と進んでください。
そしたらメネラウスの定理が完成します。
先に注意点
どちらかの耳って書いたけど、
どっちの耳を選んでも成り立つから安心してください。
そして、どっちの耳を選ぶかは、
その場で両方やって問題に合う方を使う
ようにしてな。
じゃ、具体的にそれぞれの耳のケースで見ていくで。
右耳スタートのパターン
こんなルート&式になる。
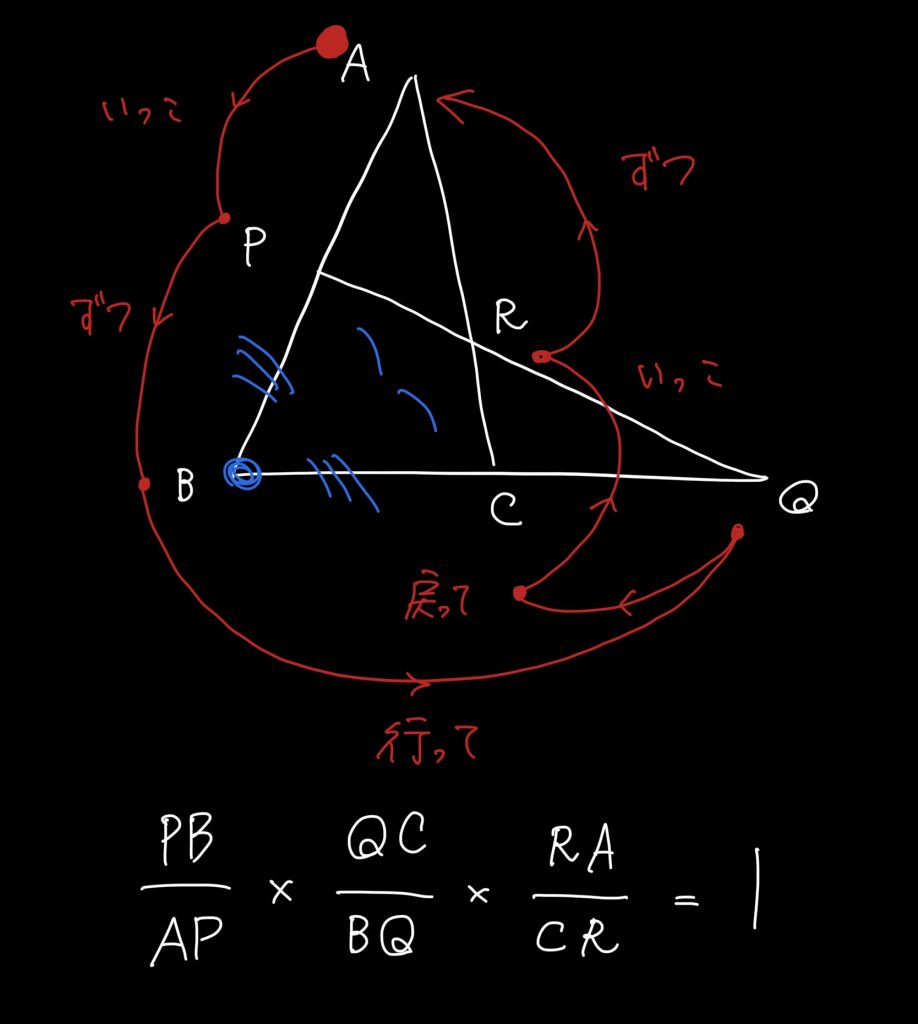
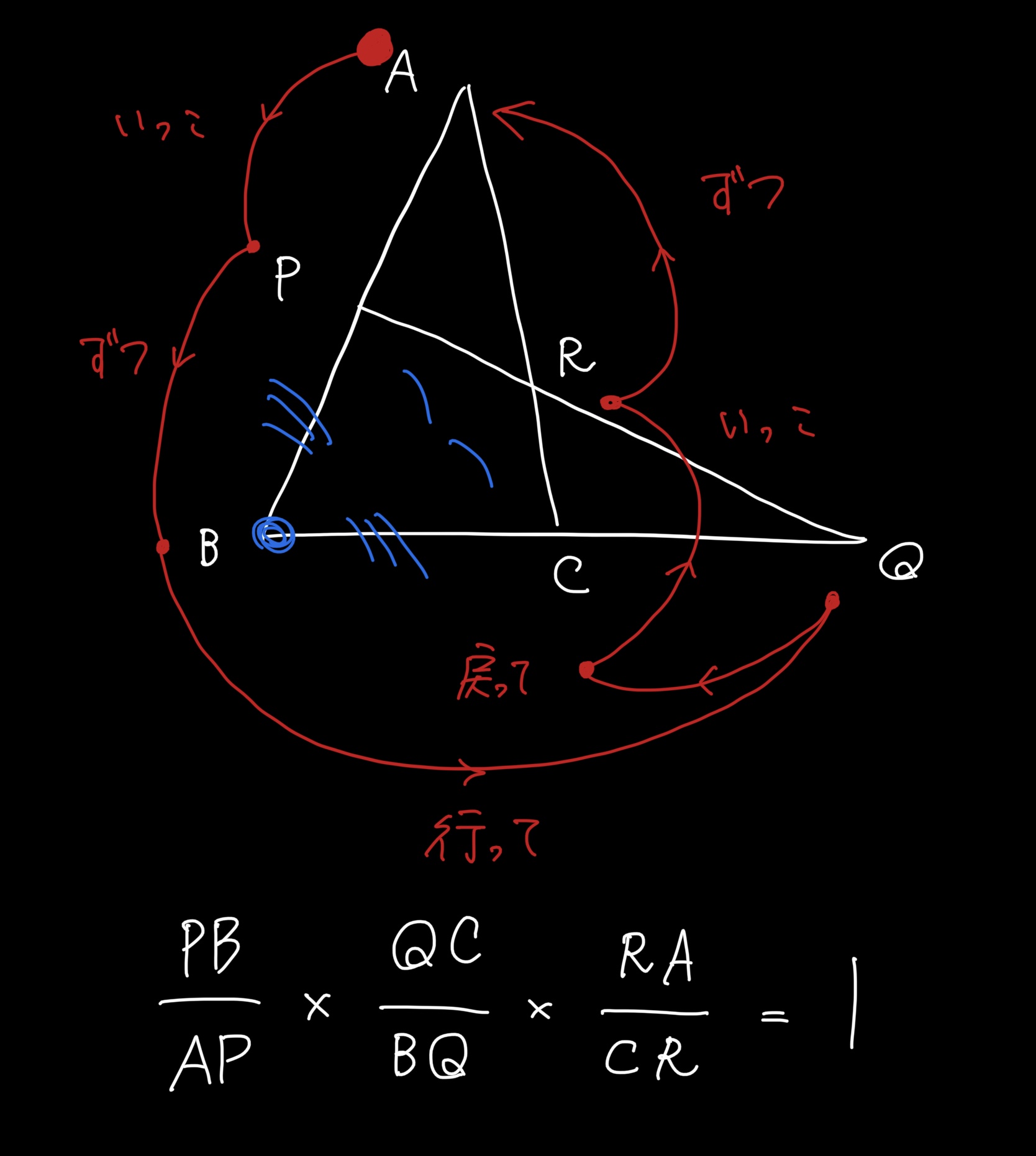
右耳→鼻で「いっこA→P ずつP→B」って唱えたら、
次にいくところが反対の耳しかない&「行って戻って」するためにはB→Qと進むしかない
から、自然と「行ってB→Q、戻ってQ→C」になるよな。
あとは、残りルートでまっすぐ「いっこずつ」するだけ。
立式するときは、諭吉が書いた式と分母分子逆になってもオッケー。
つまり、
「いっこ ぶんの ずつ」×「行って ぶんの 戻って」×「いっこ ぶんの ずつ」=1
でも、
「ずつ ぶんの いっこ」×「戻って ぶんの 行って」×「ずつ ぶんの いっこ」=1
でもオッケーってことね。
前者は覚える時ラク。
後者は書く時ラク。
左耳スタートのパターン
こんなルート&式になる。
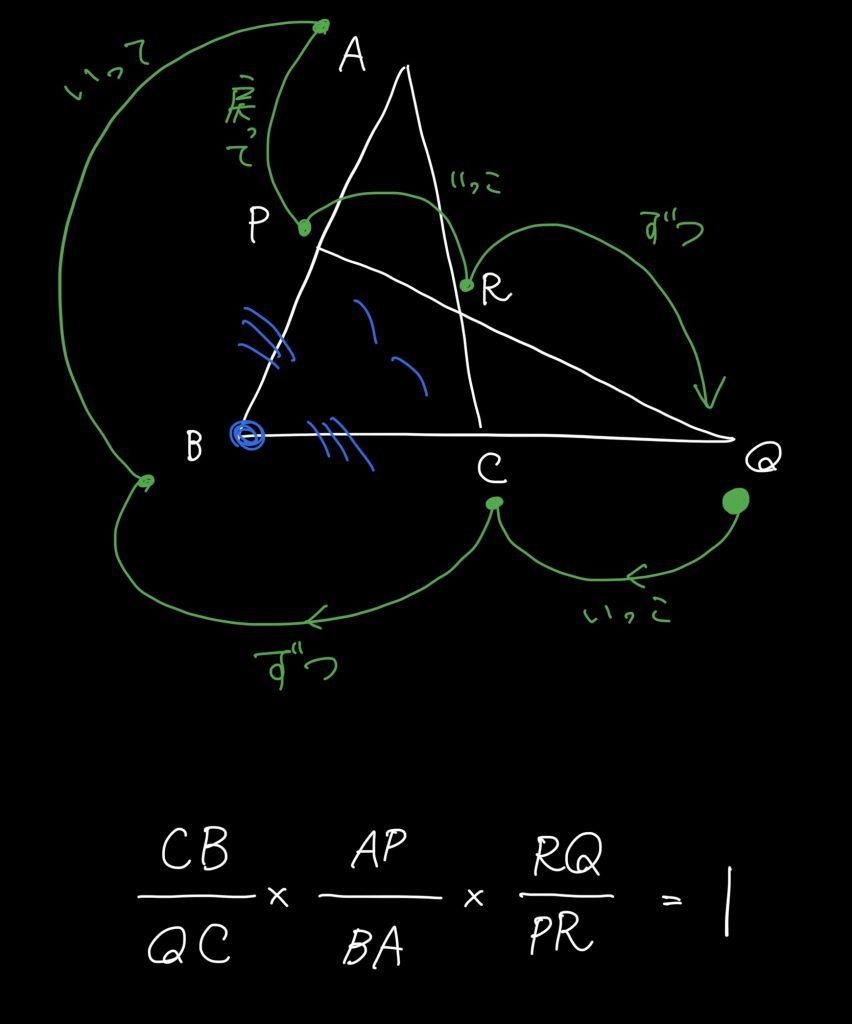
説明はもうエエよね。
ってことで、
- 使う時→キツネの顔が見えたら
- 覚え方→「いっこずつ、行って戻って、いっこずつ」
って話でした。
P.S.
あ、
そもそも作図してないとキツネの顔にすら気付けへんから、必ず作図するんやで〜!
この講座で教えた通り!