まいど!諭吉です。
『出る順』ご購入者様から、
- 2次方程式の解がx=a,bが解の時、(x+a)(x+b)ではなく(x-a)(x-b)となるのは何故ですか?
- 2次方程式の解は出せるんですけど、2次不等式の解が出せません。
というようなご質問をいただいたので、きちんとまとめたで。
これを通して、本質を理解すれば暗記は不要ってことを、感じてもらえたらうれしいなぁ!
画像はタップすれば拡大しまっせ。
2次方程式の解について
本質は小学校算数にあり!
そして2次方程式へ…
これが2次方程式の解。
まぁ、思考の中心は
小学算数の「かけてゼロなら、どっちかゼロ」
ってとこ。
2次方程式を
因数分解によってかけ算の形にして、どっちか(orどっちも)ゼロ、を求めるのが、
解を求めるってこと。
次。
2次不等式の解について
まず作図
2次不等式の解を出すには、2次方程式の解とグラフが必要ってことやな。
カッコつけて表現すると、
2次不等式の解 = 2次方程式の解 × グラフ
ってことね。
足し算じゃなくて掛け算であることに注意。
掛け算ってことは、「どっちか無ければ、全部ダメ」ってことを意味する。
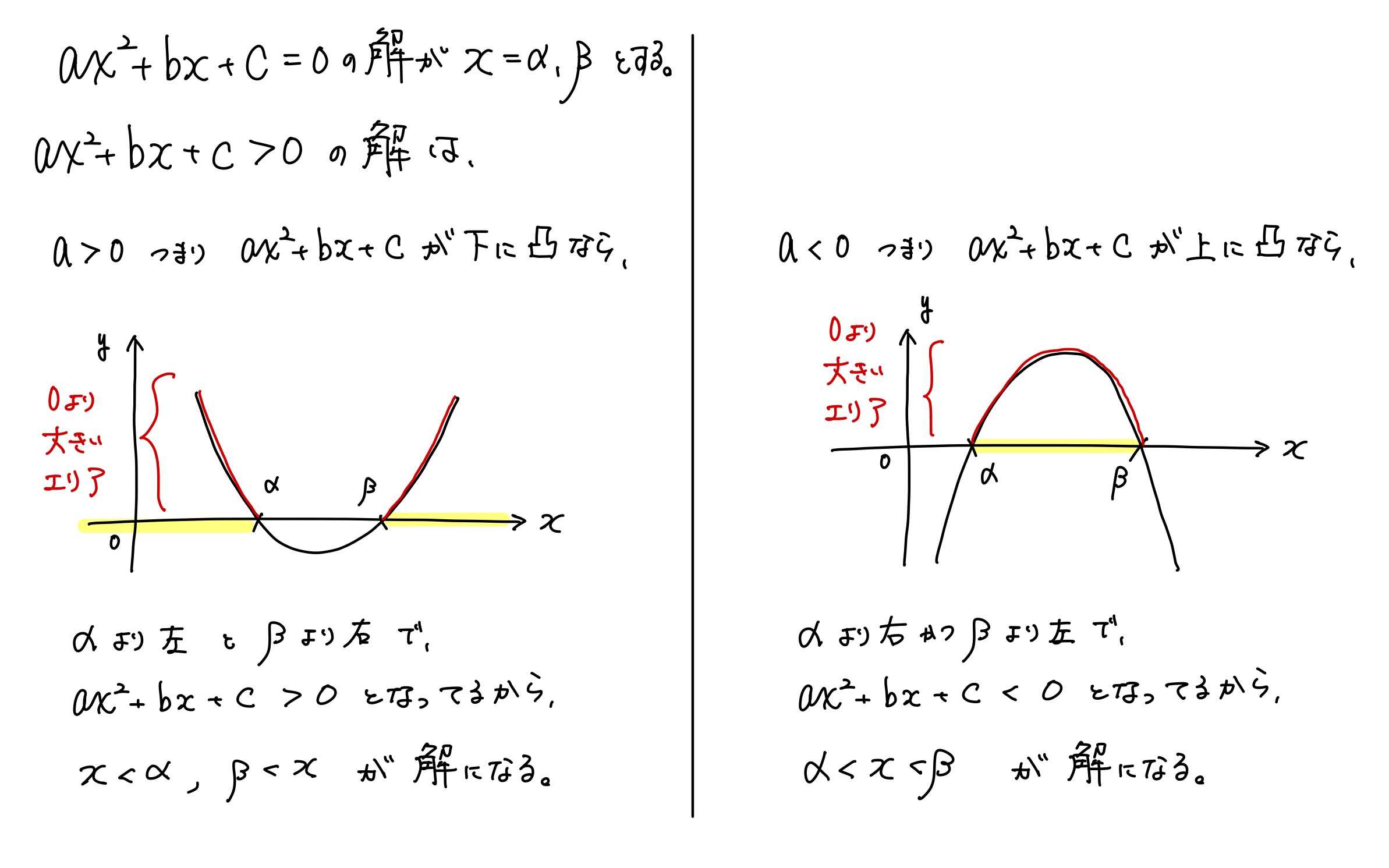
2次式>0 の解の出し方
「グラフを描いたら、赤がわかって、黄色がわかる」って順番ね。
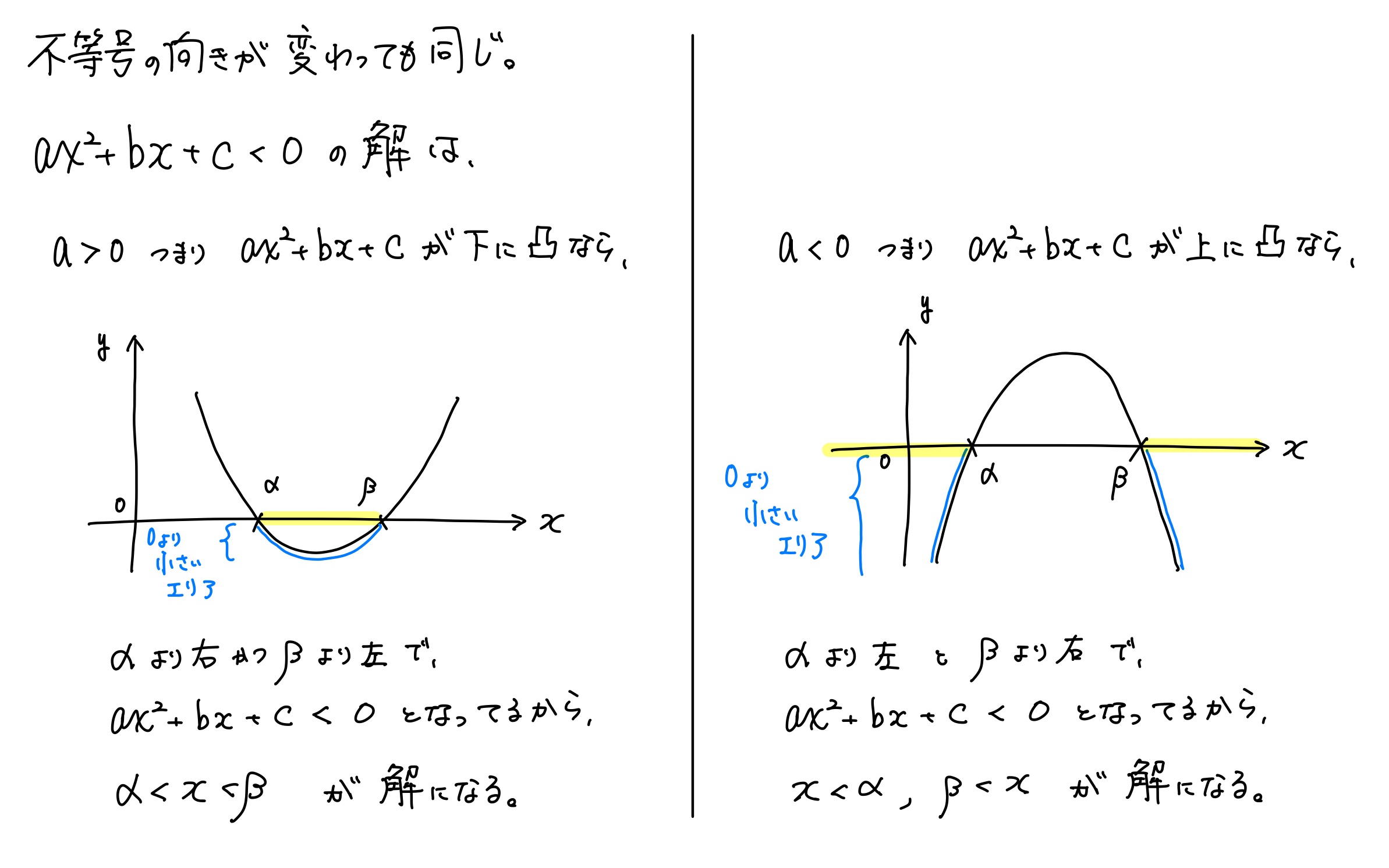
2次式<0 の解の出し方
これも、「グラフを書いたら、青がわかって、黄色がわかる」って順番。
最後に注意
ほな!
P.S.
作図しないやつは絶対伸びへんって断言してる理由、わかったかな?