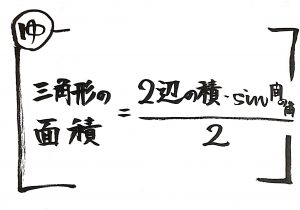お、なんやみんなアップデートするんか!?
まさかアップデート選択率100%とは!
さすが!
自主的にWebで学習するだけあるなぁ!
さて!
アップデートのためには「底辺×高さ÷2」をいっぺん忘れてもらって、
「いち にの ポカン」してもらって、
次の式を、図と一緒に覚えてほしいで。
\(S=\frac{1}{2}absinθ\)
解説するな。あ、Sは面積のことな。
…
… ゴメン!
せっかく忘れてもらったけど、思い出して!笑
実はこれも「底辺×高さ÷2」やねんな!爆笑
三角形の面積の出し方は変わらへんねん。
ただ、表現というか材料が変わってるんや。
ほんで、こっちの公式のほうが、
解ける問題のストライクゾーンが広くなるし、
こっちの公式に上書きして欲しかったから、
旧型公式を「忘れて」って表現したんや。
ほんまに忘れてしまった人、ごめんな!
さて、
この新型公式\(S=\frac{1}{2}absinθ\)を見ると、
面積を出すのに必要な「材料」は次の3つや。
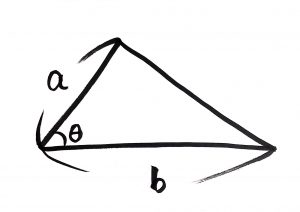
- 底辺 (今回はb)
- 他の一辺 (今回はa)
- 二つに挟まれた角 (今回はθ)
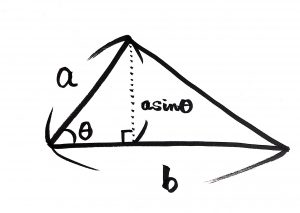
この図みたいな考え方や。
面積
=底辺×高さ÷2
=b×asinθ÷2
\(=\frac{1}{2}absinθ\)
になる。
これが便利やねんな。
しかも、さっき「底辺」とか「他の一辺」って言うたけど、どの辺でもええねん!
さっきと逆で
aを底辺、bを他の一辺(、間の角はθのまま)
と考えても、同じ式で表現できるんや。
[ごめん画像保存し忘れた笑
あとで更新するから、イメージしてみて笑]
底辺×高さ÷2
= a × bsinθ ÷2
\(=\frac{1}{2}absinθ\)
でさっきと同じ式な。
つまり…。
面積を出すのに必要な「材料」をもっとシンプルに言うことができて
- 二つの辺
- その間の角
さえわかれば面積が出せるってことになるんや。
二つの辺の積×sin(その間の角)÷2
で面積が出せるってことなんや。
ゆきちポイント
ちゅうことでまとめ!
ほな!