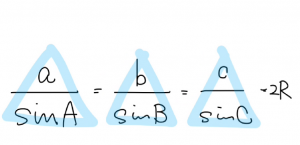まいどまいど!
三角比の重要4公式のうち
(1) \(tanθ = \frac{sinθ}{cosθ}\)
(2) \(sin^2θ + cos^2θ = 1\)
は紹介したから、残り2つを、覚えられる工夫を詰め込んで紹介するで!
まず、残り2つってなんやっていうと…
(3)正弦定理
(4)余弦定理
や。
正弦ってのはsinのことで、余弦ってのはcosのことや。
「ですから正弦定理はsinの入った方、余弦定理はcosの入っている方なのです」
とか言ってドヤ顔しとるセンセーおるけど、
そんなんで覚えられたら苦労せんわ!って話やで。笑
式と名前の一致させ方やなくて、そもそも式が覚えられへんっちゅうねん!
って話やんな笑
おっしゃ、任しといて!
その前に、数学界のマナー
あ、先に数学界の誰も教えてくれへんマナー(?)を言うとくな。
数学の世界では、
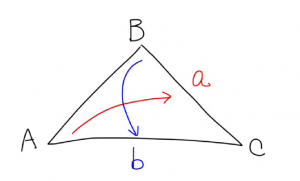
角: アルファベット大文字で表現
辺: “向かい”の角の小文字verで表現
というマナーがあんねん。
こういうことな。
“ルール”とまでは言わへんねんけど、
そうしてることが多いな。
ってことで”マナー”やで。
正弦定理
これ、覚えちゃってな。
\(\frac{a}{sin A} = \frac{b}{sin B} = \frac{c}{sin C} = 外接円の半径R×2\)
一つの式が同じアルファベットで構成されてるのはわかってもらえると思うけど、
上下ひっくり返さんようにな。
分子が小さくて分母が大きい、三角形のイメージや。
三角比の公式やから、三角形のイメージな。
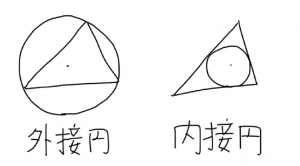
補足
外接円は、「その三角形の点すべてに外側から接するような円」のことや。
三角形が内側、円が外側な。
逆の内接円と間違わんようにな。
余弦定理
これも覚えてな。
\(a^2 = b^2 + c^2 -2bccosA\)
覚えにくいやんな。覚え方伝授するわ。
基本の形は、三平方っぽいねん。
\(a^2 = b^2 + c^2\)
そこに余計な-2bcがおんねん。
\(a^2 = b^2 + c^2 – 2bc\)
でもこれはまだ、余計とは言え理解できんねんな。
もし余計なヤツがこれだけで終わってたら、
因数分解することができてキレイになってたはずやねん。
こんな風に。
\(a^2 = (b-c)^2\)
でも、やっぱ余計なことするやつが居んねん。
よりによって急にcosAが出てきて、余計なことしよんねん。
さらに言うと、もともと余計やった-2bcに、
cosAが追い打ちをかけるようにさらに余計なことしよんねん。
\(a^2 = b^2 + c^2 – 2bccosA\)
このようにしてできたのが余弦定理や!(ドヤ顔)
…ふぅ(賢者)
こういう公式とか定理ってのは本来は、
証明をなぞって、体験して覚えるってのが一番ええねん。
公式忘れても0から作れるしな。
でも、
身近に質問できる人がおらん場合とか、
試験まで時間がない場合は、なんも考えんと覚えてもうたほうがええで。
ほな!