まいど!諭吉やで。
航空学生テキストご購入者様から
二重根号に関するご質問
をいただいたから
今日はその質疑応答をシェアするで。

いただいたご質問

この1通前に二重根号に関するご質問もいただいていました。
諭吉の返事
何度も申し訳ありません。
全然大丈夫です!
2ルート32になる意味も教えていただけないでしょか?
こんな感じです↓
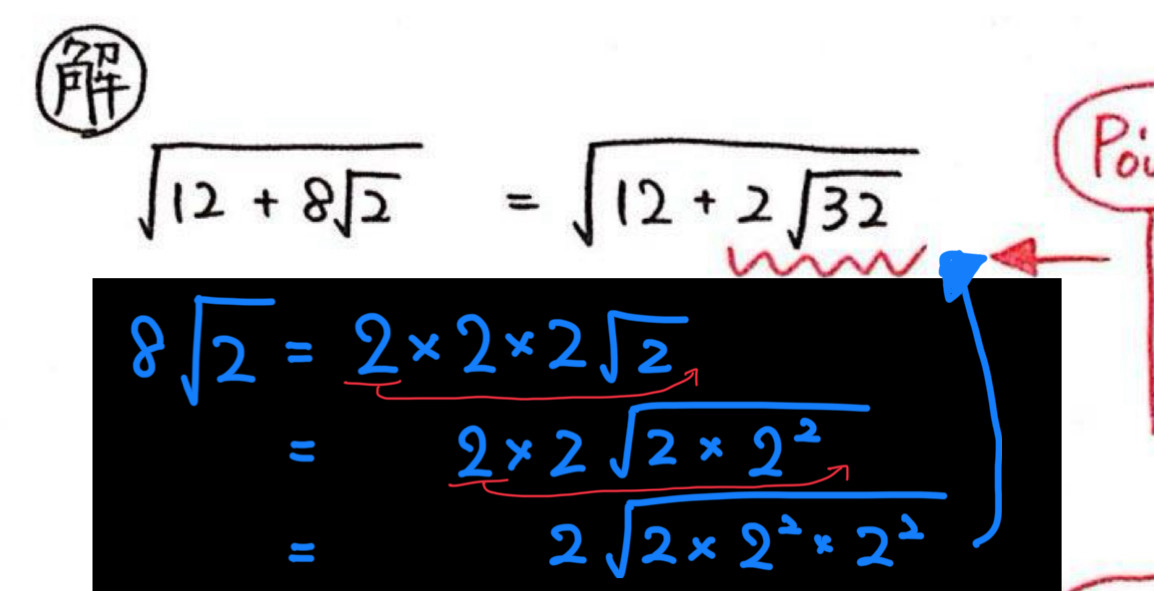
なぜ2を1つだけ残すか?というのは
二重根号の外し方に絡んできます。
二重根号の外し方に絡んできます。
二重根号の外し方は、
メインの理由はこの通りです。
メインの理由はこの通りです。

航空学生数学予想問題集より
√(●^2) = ●
という形にすることで(二重根号でいう内側の)ルートを消しています。
(このメール内でだけ「2乗でルートが消える法則」と呼びます。)
二重根号の場合は
ルートのなかにルートがあるわけですが、
とにかく外側の大きなルートの中身を
少々無理やりにでも(●±▲)^2にします。(みなします。)
なぜか?
そうすれば
√(●±▲)^2
=(●±▲)
となって外側の大きいルートが消えるからです。
「2乗でルートが消える法則」です。
そして
中身を(●±▲)^2とみなすとはどういうことか?
というと
●^2 ± 2●▲ +▲^2とみなす
ということです。
なぜなら展開公式より
(●±▲)^2 = ●^2 ± 2●▲ +▲^2だからです。
ここまでわかれば半分以上終わりです!
そして冒頭の
「2を1つだけ残す理由」
が見えてこられたかもしれません。
そうです。
(●±▲)^2 = ●^2 ± 2●▲ +▲^2の
「2●▲」を無理やり作っているということなのです。
無理やりですよねw
テキストのご質問くださった部分の先を見ていただくと
そこでも無理やりな変形が行われていますよね。
√32=√8×√4と分けたり
12=8+4と分けたり
8=(√8)^2とみなしたり
4=(√4)^2とみなしたりしています。
そうです。
これもぜーんぶ
(●±▲)^2 = ●^2 ± 2●▲ +▲^2の
を無理やり作っているのです。
√32=√8×√4と分けたり→ 2●▲ を作った
12=8+4と分けたり→次への布石
8=(√8)^2とみなしたり→●^2とみなした
4=(√4)^2とみなしたりしています。→▲^2とみなした
ということだったのです。
全ては「2乗でルートが消える法則」のため、
●^2 ± 2●▲ +▲^2とみなすためです。
無理やりすぎますよね?w
必死ですよねw
でも
人生でも恥を忍んで無理やり頑張らないといけない時もあります。
二重根号はまさにそんな時だと思ってください。w
ただ、
この無理やり感が受け入れ難い場合は
「別解」の方を使ってもらっても大丈夫です。
理屈抜きで
手順だけを
平たくいえば
こういう感じです↓
https://vt.tiktok.com/ZS2M9QRyp/
大丈夫そうでしょうか!
