熱力学(気体の問題)で、頻度高く使うものがこの2つ。
これは、覚えておいてください。
早口言葉みたいに、一気に言えるくらいまで。
前半では、気体の状態方程式についてみていったから、今度は第一法則を。
気体の状態方程式は物理でも化学でも使うけど、第一法則は物理でしか使わへんで。
熱力学第一法則:Q(in) = ΔU + W(out) について
登場人物の確認。
全部、ある気体のみを見て、各人物を考えます。
Q(in):得た熱量
3つの中で一番簡単。
\(Q_{in}\):その気体が貰った熱量(Quantity of heat)。
気体にinしてきた熱の量ってことやな。
お金で言うと、収入。
問題文でストレートに与えられているか、
そもそも、それを求めさせることが問題であることが多い。
ΔU:内部エネルギーの変化
\(\Delta U\): その気体が持っている内部エネルギーの変化。
なんでUというアルファベットで表すか?は諸説ある。が、どうでもエエ。
\(\Delta ●\)・Δ●・⊿●は全部、「●の変化量」を表す記号。
「でるた」と読みます。
⊿xは「でるた えっくす」と読むで。
変化量って日本語についてはちょっと注意が必要。
今回の場合やったら、
「気体のエネルギーは、beforeからafterへと、どうなったか?」
というのが変化。
お金で考えたらわかりやすいかな?
お金で言うと、貯金額の変化のこと。貯金に回った額のこと。
例えば、
貯金が10円から15円になった場合、貯金額の変化(貯金に回った額)は+5円。
貯金が20円から15円になった場合、貯金額の変化(貯金に回った額)は-5円。
これが変化・Δの意味。
「after ひく before」で出るわけやな。
符号もきちんと考えなアカンで。
内部エネルギーってのは、気体のmol数と温度によって決まる数値。
例えば、「単原子分子(理想気体)」の内部エネルギーは
\(\frac{3}{2} nRT\)
と表現される。(n: mol数、R: 気体定数、T:気体の温度)
これは覚えておいたほうがエエ。
気体のmol数が変わるような問題はまず無いので、「内部エネルギーの変化は、温度の変化によって決まる」と考えて
\(\Delta U = \frac{3}{2}nR\Delta T\)
とすることが多い。
W(out):気体がした仕事
\(W_{out}\): その気体がした仕事(Work)。
仕事は、外にしていくものやから、outな。
お金で言うと、支出。
そもそも仕事の算出方法は、力×移動距離やった。これは覚えてないとアカンで。
気体の場合も、同じ。
ただし、そのままじゃ使えへん。
だって気体については、いつも圧力(≠力)を考えるし、気体の移動距離ってどうやって計測するのって話。
だから、形を変えてあげる。
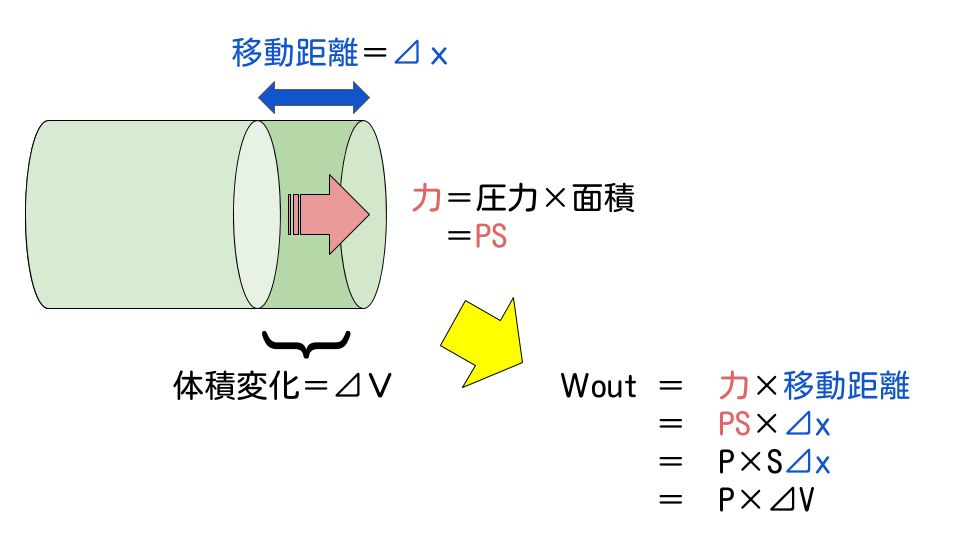
どんな形かというと、圧力×体積の変化量(P×ΔV)。
「力×移動距離」が、こんな形に変わる理由は以下。
このストーリーが頭に入ってれば、改めて覚える必要はない。
ということで、圧力Pと体積変化ΔVの掛け算によってW(out)が決まることがわかる。
よって、P-Vグラフの面積(P-Vグラフの積分)によってW(out)が出せることもわかる!(これは発展的なのでわからない人は気にしない・丸暗記でオッケー)
熱力学第一法則:Q(in)=ΔU+W(out)の使い方
ちょくちょくお金で例えてたから、
お金シリーズと並べて書いてみると…
\(Q_{in} = \Delta U + W_{out}\)
収入 = 貯金に回った額+ 支出
あら、わかりやすい。
つまりこういうこと。
「収入は、貯金か支出に回ります。」
普通やね。
もし、収入(in)が100円、支出(out)が30円なら、貯金に回った額は70円でしょ。
もし、貯金に回った額が100円、支出(out)が200円なら、収入(in)は300円でしょ。
…と、こんな風に、3人のうち2人が分かればもう1人もわかるよね、という使い方をします。
そんだけの話。
注意しないとアカンのは、
in/outはしっかり区別をつけてやってこと。
例えば、
W(out)は、気体が外にした仕事を入れないとアカンから、
「〜したところ、気体は20の仕事をされた」やったら、W(out)は、マイナス20じゃないとアカン。
Q(in)は、気体がもらった熱量を表してるから、
「50Jの発熱反応」やったら、Q(in)は、マイナス50じゃないとアカン。
ってこと。
簡単っしょ!
ほな!